Recovering weak signals¶
[1]:
import numpy as np
import corner
import pandas as pd
import matplotlib.pyplot as plt
import exoplanet as xo
import pymc3 as pm
import lightkurve as lk
[2]:
%config IPython.matplotlib.backend = "retina"
from matplotlib import rcParams
rcParams["figure.dpi"] = 150
rcParams["savefig.dpi"] = 150
Sometimes a signal is too weak to be obvious in the first_look. There are a few ways to dig deeper. One of those is the time delay periodogram module, which essentially brute forces a model for a range of orbital periods. The likelihood of the model can then be plotted against the orbital periods, and should peak at the correct value.
Let’s try this out for a short period binary, KIC~6780873
[3]:
lc = lk.search_lightcurvefile('KIC 6780873', mission='Kepler').download_all().PDCSAP_FLUX.stitch().remove_nans()
lc.plot();
[5]:
from maelstrom import Maelstrom
ms = Maelstrom(lc.time, lc.flux, max_peaks=2, fmin=10)
ms.first_look(segment_size=5);
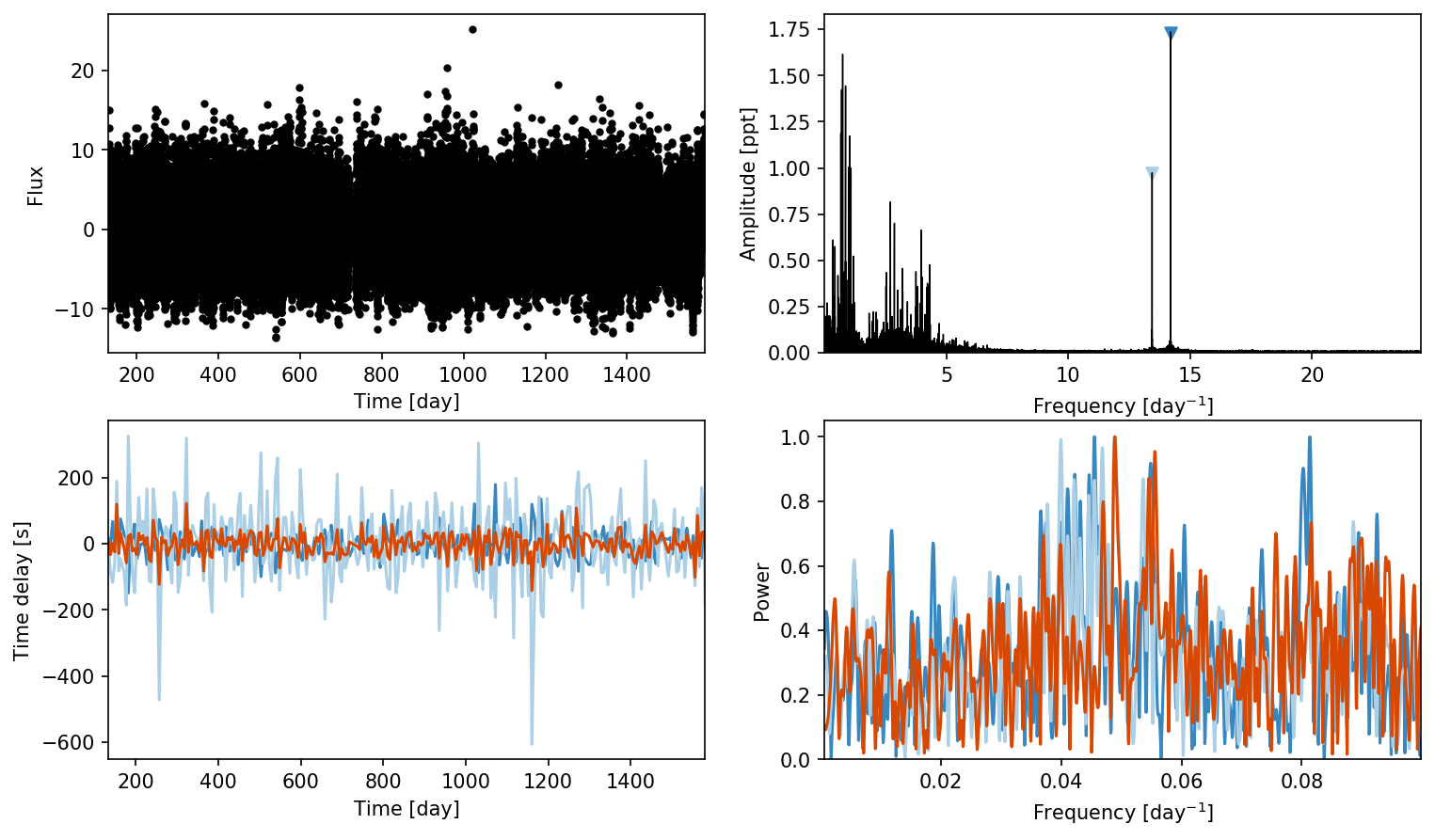
It does look like there’s something there.. but it’s hard to tell. Let’s create the periodogram searcher:
[7]:
pg = ms.period_search()
We’ll search between 5 and 15 days
[8]:
periods = np.linspace(5,15,100)
res = pg.fit(periods)
100%|██████████| 100/100 [02:51<00:00, 1.71s/it]
100%|██████████| 100/100 [03:09<00:00, 1.89s/it]
[10]:
pg.diagnose();
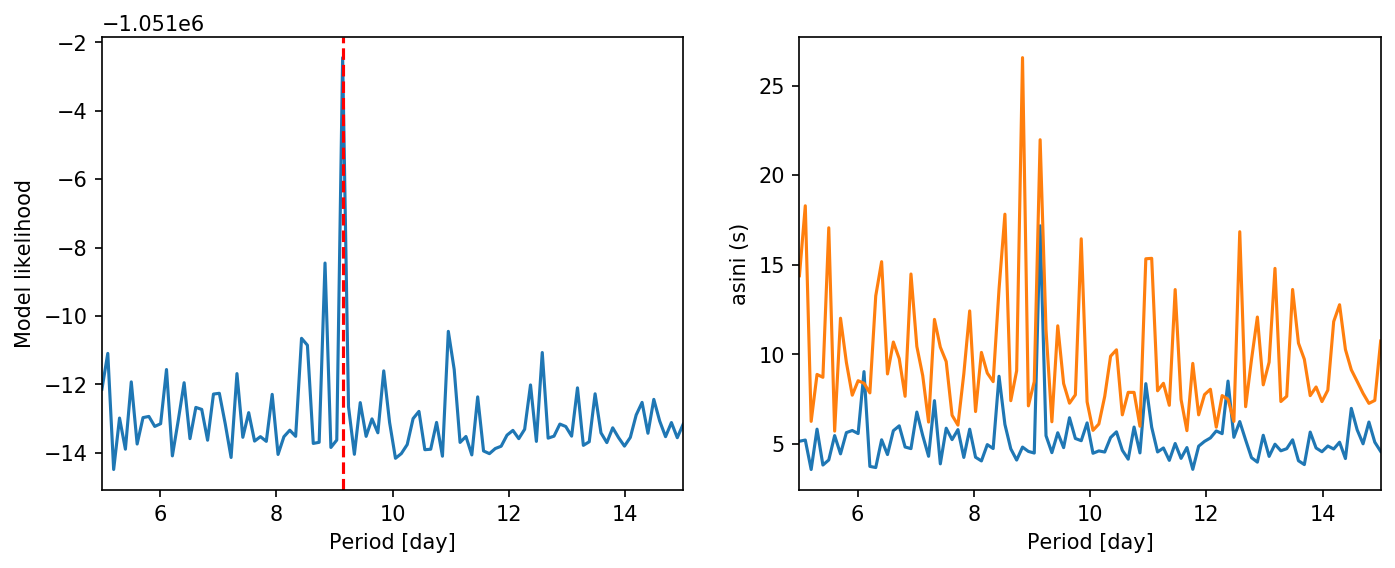
Cool, there’s a peak at the orbital period of ~9 days! This is almost exactly where we know it to be. The contents of the pg.fit results are a list of optimisation dict results. If we want to make these plots manually, we can do the following:
[15]:
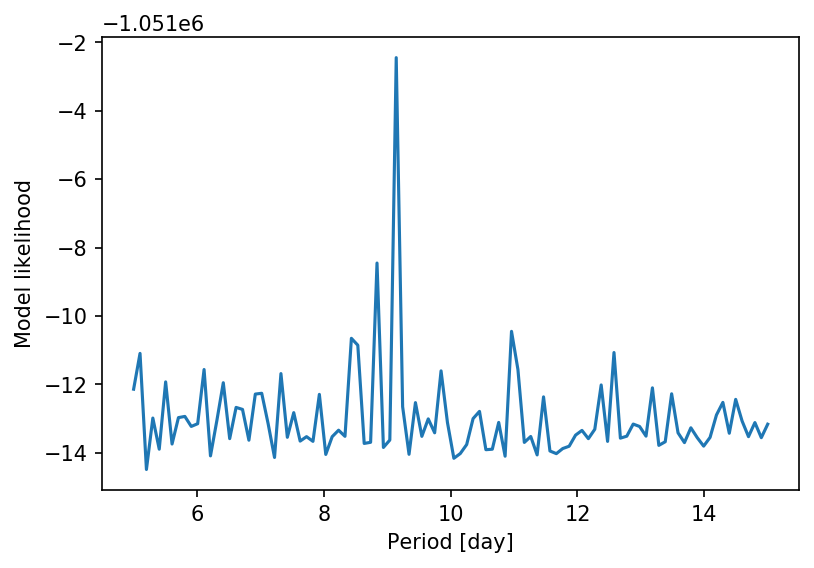
ys = np.array([[r[0] for r in row] for row in res])
sm = np.sum(ys, axis=0)
plt.plot(periods, sm)
period = periods[np.argmax(sm)]
plt.xlabel('Period [day]')
plt.ylabel('Model likelihood')
print(f"Expected orbital period at {period:.2f} days")
Expected orbital period at 9.14 days
[ ]: